船舶穿上鲨鱼皮，仿生科技解锁航行新速度

仿生结构减阻性能理论计算和试验研究

王宗永

（南京佳乐船舶设备有限公司，江苏 南京210000）

摘要

船舶减阻技主要解决船体表面运行阻力大的问题。本文参考仿生学，以鲨鱼皮表面盾鳞结构为研究对象，通过简化该结构，并设计合适参数，打印至基板上，制成仿生膜。采用CFD数值模拟计算出该仿生膜的理论减阻率；最后，根据仿生膜设计参数，采用循环水槽模型试验，测算出该仿生膜的实际减阻率。

【关键词】船舶减阻；仿生膜；模拟计算；减阻率实测

减阻技术的发展对节能减排、经济增长以及海洋强国建设均具备重要意义。所谓减阻，即减少表面摩擦阻力。船舶航行产生的阻力包括摩擦阻力、兴波阻力、黏压阻力以及其他阻力。船舶航行时，船体表面的摩擦阻力占总流体阻力的绝大部分(对货船而言，表面的摩擦阻力超过总航行阻力的60%)。已有研究表明，若能将船舶表面遇到的水阻力减小10%，其速度和航程将增加3.57%。因此，如何采用合适的手段减小船体表面运行阻力是航运领域亟需解决的问题。

一、研究背景

目前，仿生超疏水减阻技术存在较大的开发空间。受到鲨鱼皮表层盾鳞以及盾鳞上微型肋状沟槽结构的启发，发现微沟槽结构可以改变湍流边界层内的水流状态，诱导流体发生平行于流向的滑移来降低剪切应力，从而表现出良好的减阻效果。

现阶段，针对仿生结构的研究，较多学者从鲨鱼、贝壳、珊瑚等生物表面提取不同微结构，通过数值模拟对仿生结构的减阻效果进行计算分析，并展开了减阻机理研究。例如：令狐克骑等将仿鲨鱼皮表面结构应用到三维翼型上，通过数值模拟探究了布置面、雷诺数、所处位置和排列方式对翼型水动力性能的影响。高美红等以短鳍灰鲭鲨为仿生模本，探索了特征部位鳞片参数与周围流场之间的关系规律。李永成等系统地分析了沟槽形状、几何尺寸等参数对减阻性能的影响。Ibrahim 等通过计算机辅助设计(CAD)软件对盾鳞结构简化构建,获得了刀刃形的曲面盾鳞结构，模拟结果表明，阻力系数下降了3.75%。

上述研究主要集中在仿鲨鱼皮表面结构和减阻率的数值模拟上，鲜有相关文献报道进行实验论证。本文在简化后的盾鳞结构模型基础上重新设计了仿生膜的结构参数；采用CFD数值模拟计算出该仿生膜的理论减阻率；最后，根据仿生膜设计参数，采用循环水槽模型试验，测算出该仿生膜的实际减阻率。

二、仿生膜结构设计

2.1盾鳞结构简化过程

参考前人对鲨鱼皮特征部位鳞片的预处理方法，制备鲨鱼皮样品。从扫描电子显微镜图像(SEM图，见图1)可以看出，鲨鱼皮样品表面具有密集的凹槽结构，凹槽结构沿着流向分布。更具体地，观察单个鳞片可以发现：鳞片表面由凸起的肋脊构成。

图1.鲨鱼皮样品表面的SEM图

鲨鱼皮表面的盾鳞结构复杂，不论是直接进行仿真模拟还是生产，均存在较大的难度。因此，如图2所示，以复杂盾鳞结构作为建模基础，简化其特征形貌，将复杂结构转化为五个不同长度的肋脊，即作为本文的仿生膜结构模型。

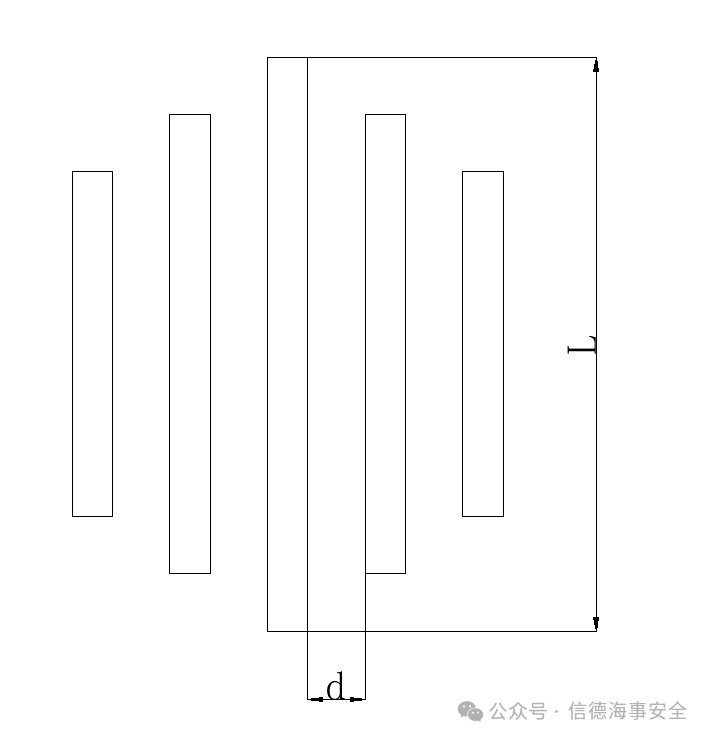
(c)简化后的盾鳞结构

图2.盾鳞结构模型简化过程

2.2仿生膜参数设计

基于实际使用需要，仿生膜的设计参数如下：仿生膜由多个盾鳞结构单元组成，每个盾鳞结构单元包括五根脊和4个沟槽，单根脊的长度L由中心向外依次为2.5mm、1.5mm和0.5mm，单根脊的宽度w为0.1mm，单根脊的高度均为0.2mm，相邻两根脊之间的间距(即沟槽宽度)d为0.1mm。

如图3所示，盾鳞结构单元有如下2种排布方式：对齐排布和交错排布。

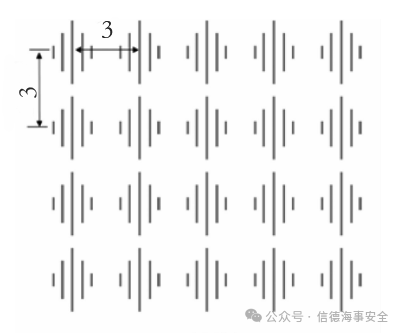
(a)对齐排布

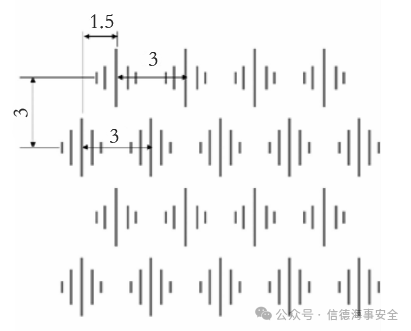
(b)交错排布

图3. 简化后的盾鳞结构排布方式(图中单位为mm)

为了进行实际减阻率测算，根据上述参数，采用固化树脂在平面基材上打印出简化后的盾鳞减阻结构，制成仿生膜样品。如图4所示，图4为实际生产出的仿生膜样品图，从图4中可以看出，仿生膜样品选择了交错排布的盾鳞减阻结构，每个盾鳞减阻结构中心脊之间的横向间距和纵向间距均为3mm。盾鳞结构与基材边缘处的距离为1mm。

图4.仿生膜样品图

三、减阻率理论模拟

本文以上述仿生膜样品图作为数值模拟对象，设置流体域和边界条件、选择合适控制方程，采用网格划分提高仿真模拟的计算精度；最后，监测不同流速下，仿生膜表面和光滑表面在相同高度处的速度云图和剪切力云图，探究流速与仿生膜减阻率之间的关系。

3.1数值模拟

3.1.1流体域的创建和边界条件确定

为了便于比较，对所有非光滑表面建立相同的流体域，并将非光滑表面和光滑表面置于同一流体域内。如图5所示，本文设置流体域的范围为：流向长度为34.5mm，展向长度为39.6mm；经过对比不同高度流体域的速度场和压力场，当垂向高度≥10mm时，光滑表面处的流体的流动状态不受到仿生膜表面流体的流动状态影响，从而保证了两个表面之间的模拟结构相互独立。因此，流体域的垂向高度为10mm。

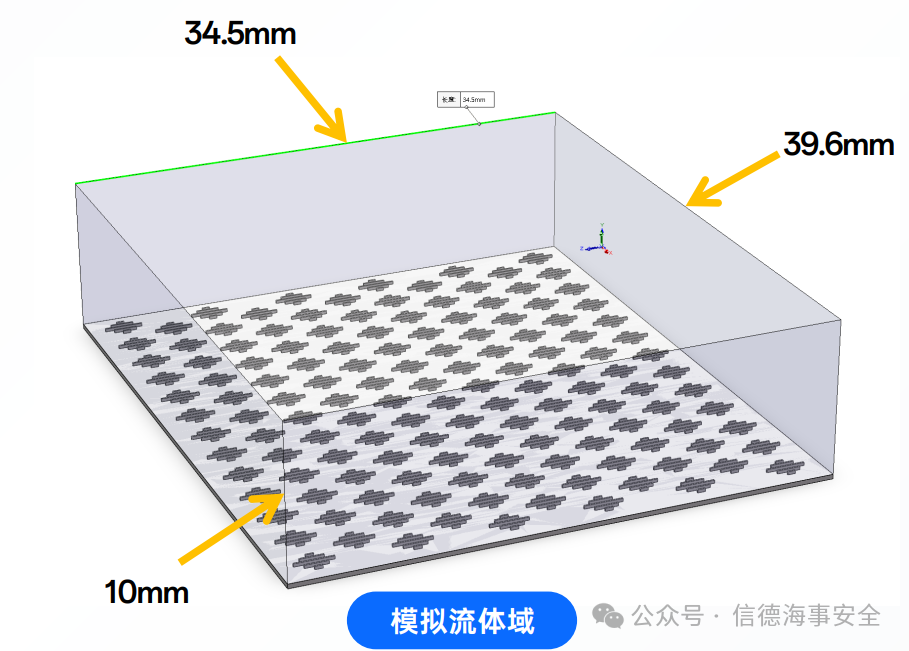
图5.流体域创建参数

采取的边界条件如下：

第一，入口边界条件为速度入口，基于船舶航行的真实速度，入口流速分别设置为3m/s、5m/s、8m/s三个工况；出口边界条件设置为压力出口；

第二，流体域垂直于水流方向的两侧壁面的边界条件设置为对称边界条件；

第三，光滑上表面和仿生膜表面设置为无滑移壁面边界条件；

第四，设定每时间步迭代50次，以保证流场充分发展。

3.1.2控制方程和湍流模型选择

运用雷诺平均数值模拟方法模拟流场的流动，流体域设定为不可压缩流体的定常流动，对应的控制方程如下：

质量守恒方程为；

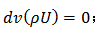
动量守恒方程为

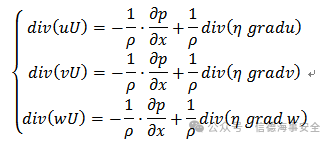
上述公式中：ρ为流体密度，u、v、w为速度矢量沿流体域x、y、z轴的速度分量，p为压强，η为流体动力粘度。

同时，由于非光滑微结构的尺寸量级小，有可能造成粗糙壁面附近压力的较大波动，并且流体域纵向的高度较大，在远离壁面的中心区域又存在充分发展的流区，湍流模型选择SST k-w模型，在近壁区域模拟计算中，能够获得更加准确的结果。该模型中所有方程的收敛残差为10-4。

3.1.3网格划分

由于仿生膜表面的盾鳞结构尺寸小且数量多，因此，采用混合网格进行区域离散化，即，如图6所示靠近非光滑表面用非结构化网格,其他区域采用结构化网格划分。

图6.网格划分

图6中，绿色部分为结构化六面体网格，黄色部分为四面体网格。四面体网格能够充分适应仿生膜表面的盾鳞结构，提高计算精度。而靠近光滑表面采用结构化六面体网格，排布规整，计算收敛效率高。

一般而言，网格越细，计算结果越接近实际流动状态。但网格数目越高，对计算设备的要求也越高，计算时间对应增长。因此，综合考虑模拟准确性和所需的计算成本，参考相关文献中选择了划分出465万的网格，本文最终划分网格数约681万，对仿生膜进行后续数值模拟。

3.2模拟结果

基于上述模拟参数设定，在仿生膜表面和光滑表面上方相同高度上（取脊结构的半高0.1mm）监测速度云图和剪切力云图。

3.2.1流速3m/s工况下的减阻效果

图7-8分别对应流速为3m/s工况下的仿生膜表面以及光滑表面的速度云图和剪切力云图。

图7.流速3m/s下仿生膜表面以及光滑表面的速度云图对比

(a)仿生膜表面剪切力云图

 (b)光滑表面剪切力云图

图8.流速3m/s下仿生膜表面以及光滑表面的剪切力云图对比

通过图7和图8可知，由于流动边界层的存在，在3m/s的入口流速下，距光滑表面0.1mm处流速只有约1～1.5m/s，而在仿生膜结构表面的相同高度上，在脊结构的周围出现了流速2～2.5m/s的区域。该仿生膜具备减阻效果。

同时，在前两排脊结构的迎风面上出现较高的剪切应力，而在流体绕流后的其余位置，表面剪切应力显著降低，甚至低于光滑表面产生的剪切应力。

根据剪切力云图可以绘制出剪切力随流动时间变化曲线，见图9。

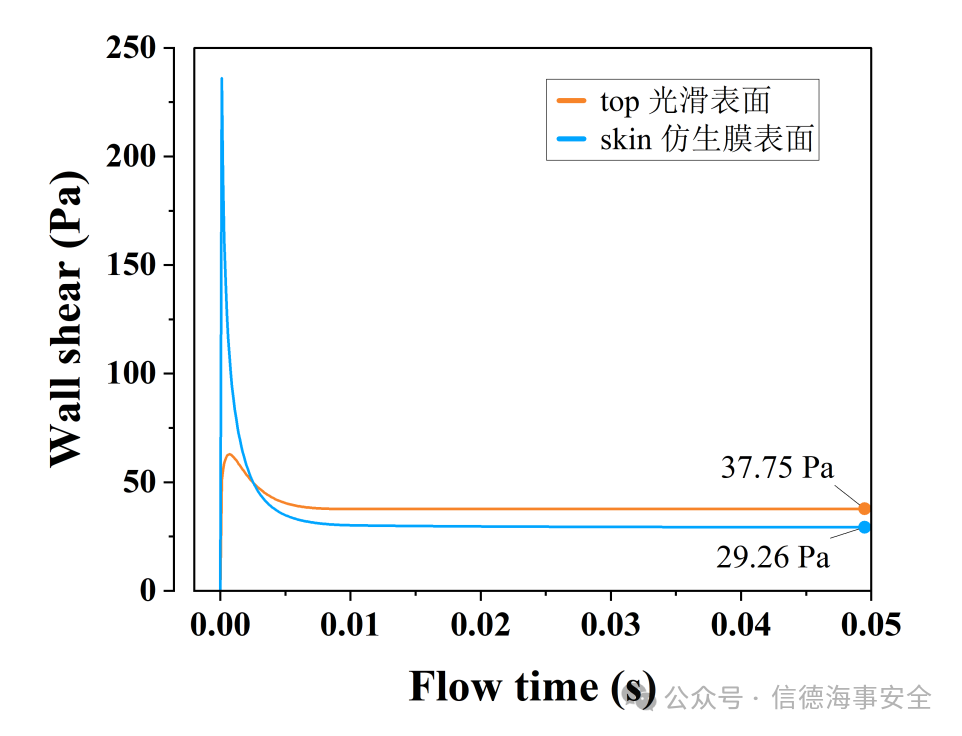
图9.剪切力随流动时间变化曲线

根据图9可知：

1.在流动开始的初期，仿生膜表面的壁面剪切力迅速增加，峰值高于光滑表面，而在流动稳定后比光滑表面的剪切力更低。

2.计算出3m/s流速工况下，仿生膜减阻率约为22.5%。

3.2.2流速5m/s工况下的减阻效果

图10-11分别对应流速为5m/s工况下的仿生膜表面以及光滑表面的速度云图和剪切力云图。

图11.流速5m/s下仿生膜表面以及光滑表面的剪切力云图对比

通过图10和图11可知：

在5m/s的入口流速下，距光滑表面0.1mm处流速只有约1.8～2.4m/s，而在仿生膜结构表面的相同高度上，在脊结构的周围的区域流速可达3～3.6m/s。

5m/s下的表面剪切力情况与3m/s表面剪切力情况类似。

根据剪切力云图可以绘制出剪切力随流动时间变化曲线，见图12。

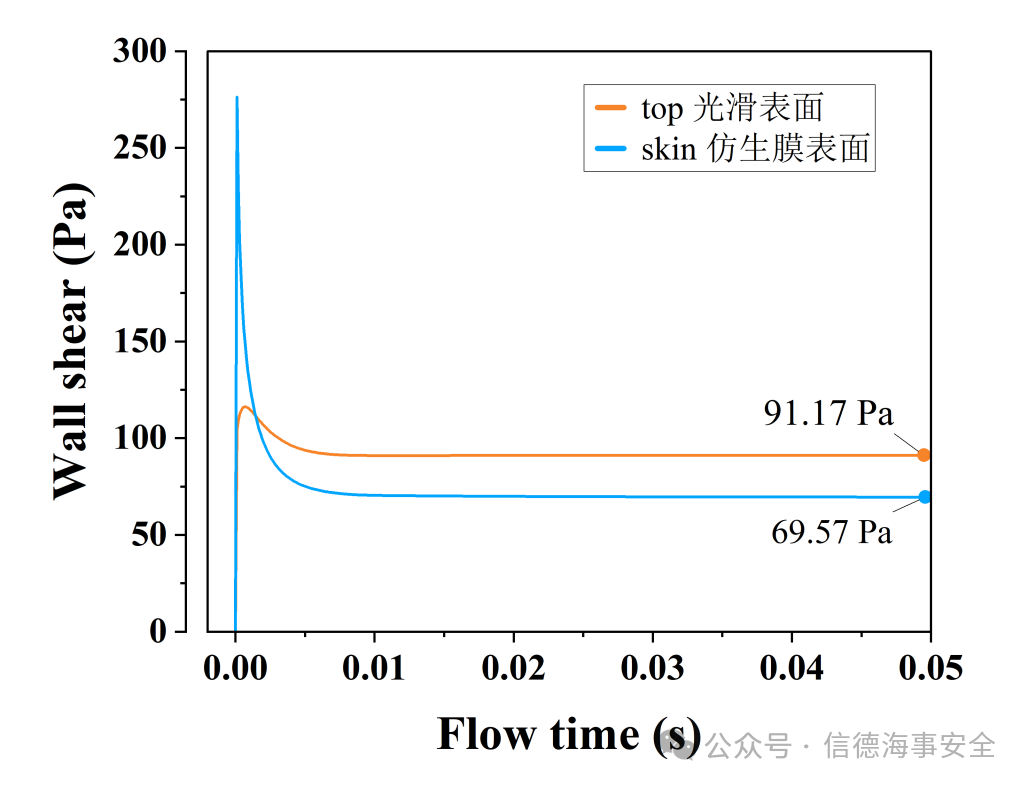
图12.剪切力随流动时间变化曲线

根据图12可以计算出：5m/s流速工况下，仿生膜减阻率约为23.7%。

3.2.3流速8m/s工况下的减阻效果

图13-14分别对应流速为8m/s工况下的仿生膜表面以及光滑表面的速度云图和剪切力云图。

图14.流速5m/s下仿生膜表面以及光滑表面的剪切力云图对比

通过图13和图14可知，8m/s流速下，仿生膜表面上，脊结构周围的流速为光滑表面的流速的1.2～1.25倍。8m/s流速下，位于流向后方的脊周围剪切力仍然比光滑表面的值更低。

根据剪切力云图可以绘制出剪切力随流动时间变化曲线，见图15。

图15.剪切力随流动时间变化曲线

根据图15可以计算出：8m/s流速工况下，仿生膜减阻率约为26.1%。

3.3结论

通过上述减阻率计算结果可以看出：

第一，随着入口流速的增加，光滑表面的速度约为入口流速的一半甚至更低，光滑表面的速度损失大；而仿生膜表面的速度约为入口流速的75%～83%，仿生膜表面的速度损失小，减阻效果优异。

第二，仿生膜减阻中，脊的迎风面上出现较高的剪切应力，后方剪切力值低于光滑表面；与光滑表面相比，仿生膜能够更好地控制壁面剪切力的范围，从而实现减阻效果。

第三，仿生膜的减阻率随着入口流速的增大而增加，在高流速下，仿生膜能够获得更优的减阻性能。

四、减阻率实际测算

本文采用循环水槽模型试验，测试管路为仿生膜表面的管道和光滑表面的管道，并代入计算公式可以得到实际减阻率。

4.1测试原理

对于不可压缩黏性流体的管道流动, 能量耗散主要来源于流体内部的黏性耗散，并可由水头损失来表示。水头损失可根据水头形式的伯努利方程(1)求得:

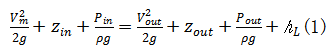
对于水平放置的直管内的定常流动, 式(1)可简化式(2)，具体如下：

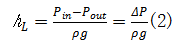
式中：为管道入口流速；为管道出口流速；为入口高度；为出口高度；为入口压力；为出口压力；为水头损失。通过测量流体流经不同壁面管道两端的压力差，可以直观地表示不同壁面的减阻能力。本文通过测试带有简化后盾鳞结构的管壁表面压差和光滑管壁表面压差，按照式(3)计算出实际减阻率：

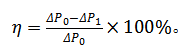
4.2循环水槽模型

如图16所示，测试系统由水泵、水箱、入口稳流段、测试管路连接构成水循环系统。通过差压变送器测量试验段两端的压差。

采用超声波流量计测量水的流速以及流量。

所有数据汇集到电气控制箱内，人机交互通过可编程触摸显示屏实现。水泵选用GRUNDFOS CM10-2型离心泵，额定流量为10m3，额定扬程为27.1m。

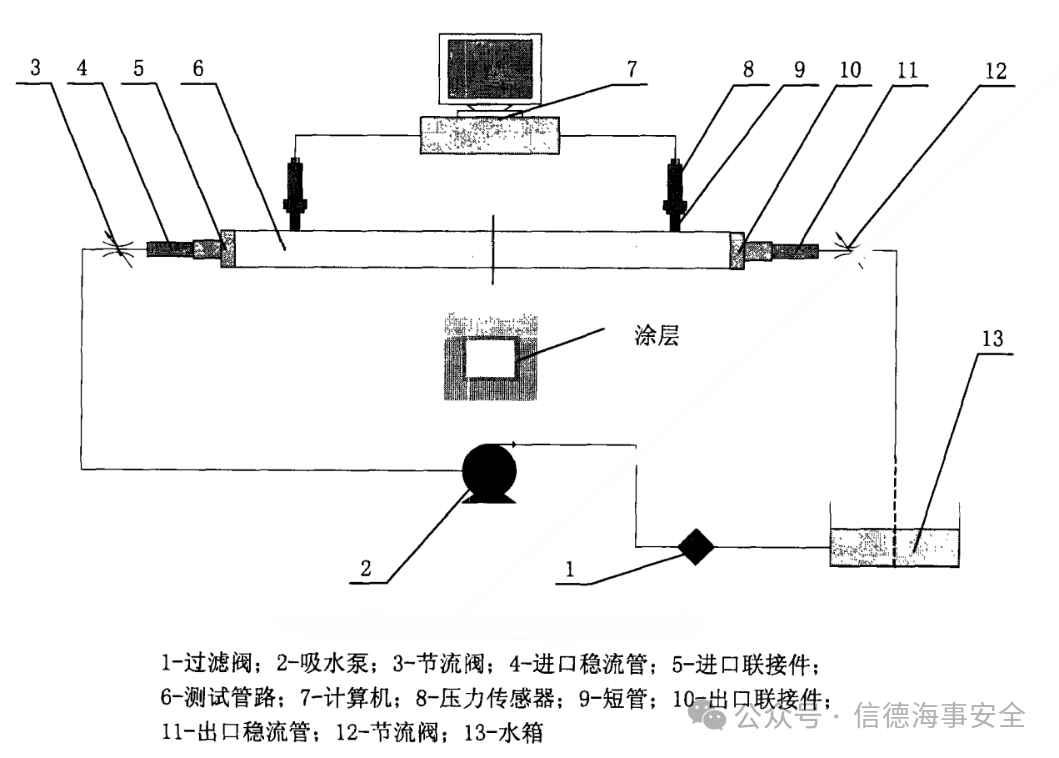
图16. 循环水槽模型测试系统

如图17所示，基于上述循环水槽模型测试系统，本文安装了测试装置。以下是测试装置的多个不同角度、不同部位的实景图。图17中，(a)体现了水箱、测试管路、差压变送器以及超声波流量计安装的位置关系；(b)为差压变送器以及超声波流量计实时监测图；(c)为测试管路图，本文采用的测试管路外径为140mm，内径为130mm，长度为90cm。

图17.测试装置图

在不同入口压强下，通过压力传感器自动测量、实时显示进、出口测试面上的压强及进、出口测试面间压强差的大小。计算机测试程序(Drag-reducing测试程序)自动连续记录处理压力传感器采集的数据，提供流阻性能测试结果。

测试装置及计算机采集系统的使用方法如下：

(1)安装实验装置，包括测试管路的安装、联接件、截留阀、导液管、泵的联接等；

(2)安装压力传感器、超声波流量计及计算机测试部分；

(3)测试前先开机预热10分钟，然后使用；

(4)试验开始前在计算机中进行有关参数设定，如采集周期、试验周期等；

(5)调节出口端节流阀用以控制进口水流的压强；

(6)开始试验，到达试验周期时，试验自动结束。中途若需要终止试验，可以存盘退出；

(7)显示输出，可以同时显示进、出口电压值；

(8)试验完成后保存试验结果；

特别要注意的是测试平台上应标记管路的安放位置,并且每次试验前应用水平尺进行标定以确保测试管路的正确安放，即要严格保证安放位置的同位性和管路的水平度。

4.3试验方法

试验条件：所有试验在环境温度15℃下进行，流体介质为水，试验后压差值的取值为计算机数据处理结果中压强值稳定阶段的进、出口测试面间的压强差。

试验数据：相同条件下，重复做三次试验，以保证试验数据的真实性和准确性。

试验记录：

1)以带有简化后盾鳞结构表面的管道为试验对象，通过改变测试水流量，改变水的流速，记录进口压力和出口压力，从而计算出不同流速下的进出口压差。计算结果见表1。

表1.带有简化后盾鳞结构表面的管道中水流速对进出口压差的影响

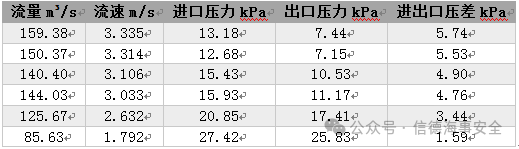
2)以光滑表面的管道为试验对象，通过改变测试水流量，改变水的流速，记录进口压力和出口压力，从而计算出不同流速下的进出口压差。计算结果见表2。

表2.光滑表面的管道中水流速对进出口压差的影响

针对表1和表2记录数据，代入至式(2)中，得到压差与流速之间的关系，并绘制成折线图，折线图为图14。图14中，黄色折线反映光滑表面的流速和压差之间的关系；蓝色折线反映仿生膜表面的流速和压差之间的关系。

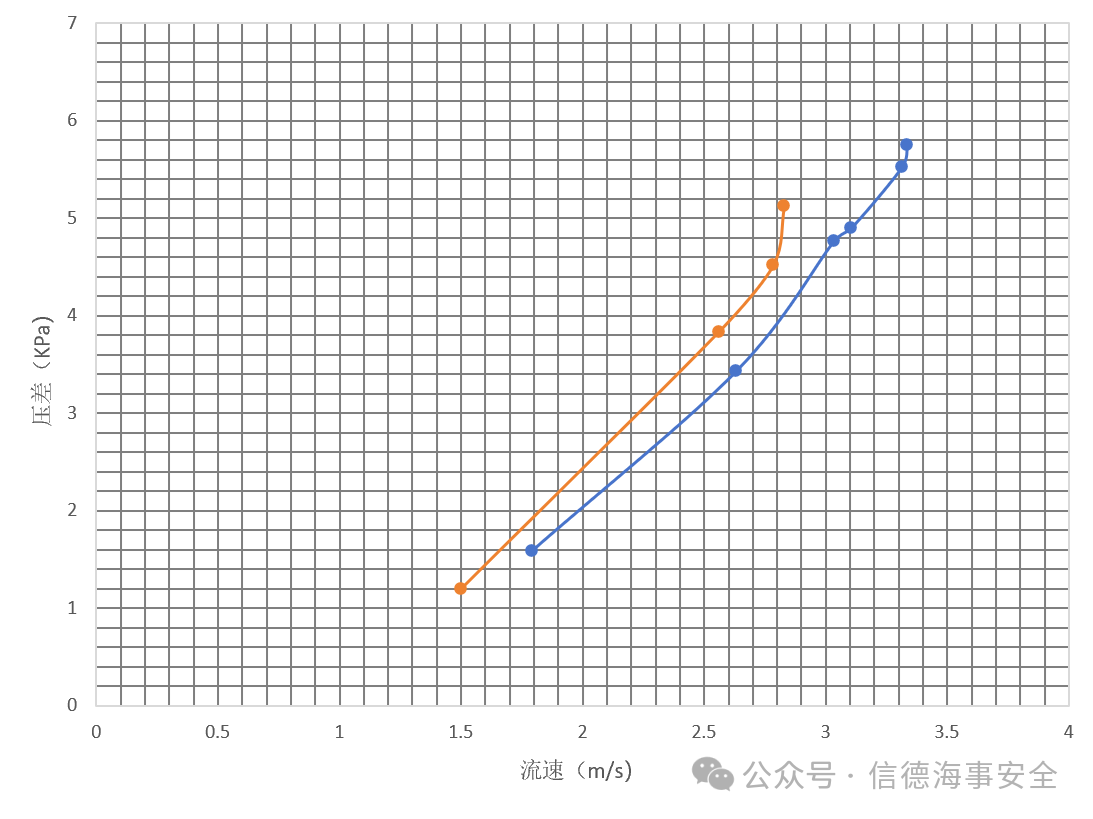
图18.压差与流速关系图

根据图18，将压差换算成阻力值，可得到流速与阻力值之间的关系，并绘制成折线图，折线图见图19。图19中，黄色折线反映光滑表面的流速和阻力值之间的关系；蓝色折线反映仿生膜表面的流速和阻力值之间的关系。

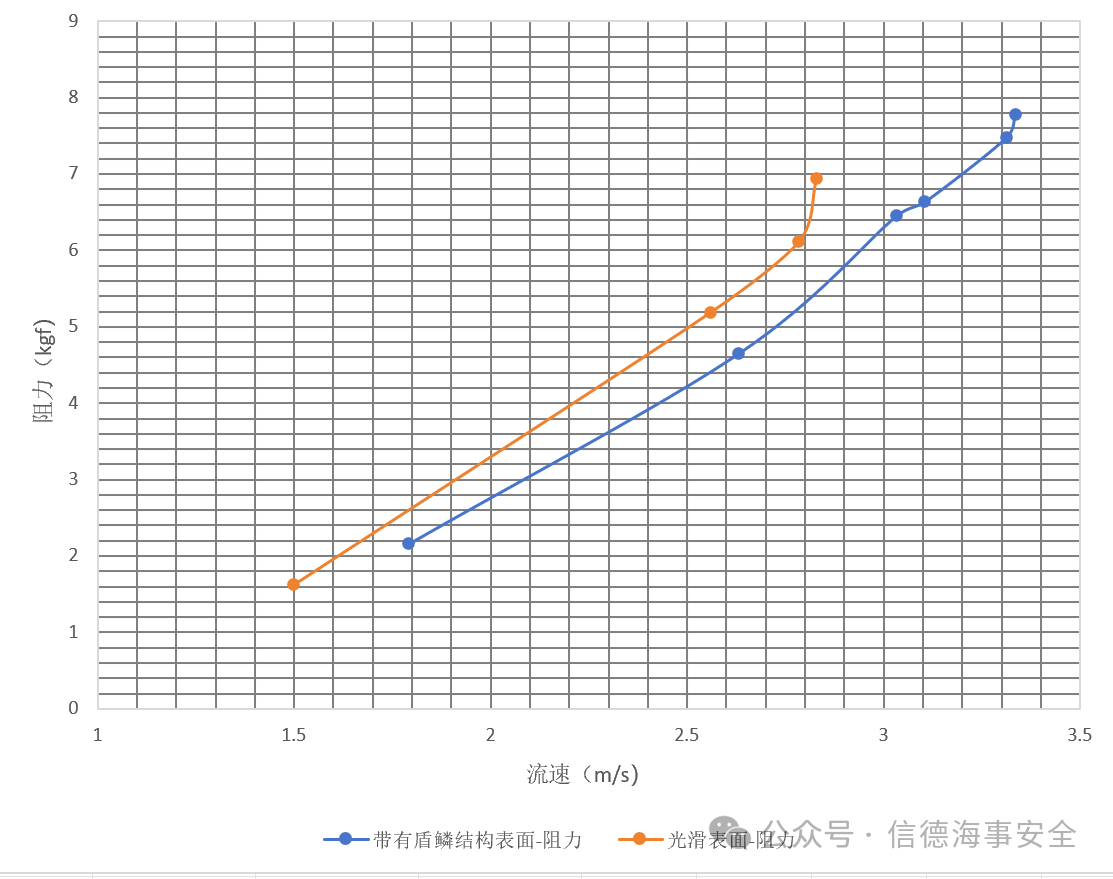
图19.阻力值与流速关系图

4.4试验结果

根据图19记录的数据，以2.56m/s的流速为例，同一流速下，仿生膜表面的管道所受阻力值约为4.2kgf，光滑表面的管道所受阻力值为5kgf。代入式(3)可以得到减阻率=(5-4.2)/5×100%=16%。

五、结论

第一，本文依据鲨鱼皮表面结构，简化形成仿生盾鳞结构，该盾鳞仿生结构的作用机理如下：水流经过盾鳞的结构后产生的漩涡，该漩涡可以理解为“微空气轴承”。这种结构改变了水流与船体表面的摩擦力作用方式，由“滑动摩擦”变为了“滚动摩擦”。经过我们水流实验表明，流速在2.5m/s时，试验减阻率为16%，随水流速度增加，减阻率也相应提高。

同时，根据实际生产需要，本文设计仿生膜的盾鳞结构单元的脊长为0.5～2.5mm，脊宽为0.1mm，脊高为0.2mm，同一盾鳞结构单元的沟槽之间的间距为0.1mm；盾鳞结构单元与基材边缘之间的距离为1mm，相邻盾鳞结构单元之间的展向距离和流向距离均为3mm，盾鳞结构单元以交错排布的方式排列；基于上述设计参数，本文制成了仿生膜样品；该仿生膜减阻技术可以应用于油运运输、舰船、水下航行器、流体机械等领域。

第二，本文采用CFD数值模拟方法，探究了仿生膜在不同流速下理论减阻率的变化，具体为，流速增加，仿生膜的理论减阻率越大；入口流速控制在3～8m/s时，仿生膜的理论减阻率可以达到22.5～26.1%。

第三，根据实际试验检测结果可知，该仿生膜在2.56m/s的入口流速下减阻率达到16%；流速提升至5m/s时，减阻率可以达到20%以上。仿生膜的理论减阻率和实际减阻率相适配。

参考文献：

[1]赖昭,郝宇,姜晨.鲨鱼盾鳞仿生表面单元结构优化及减阻性能研究[J]. 舰船科学技术, 2024, 46 (20): 50-55.

[2]徐成宇,王永华,焦远东,等.仿生鲨鱼皮表面的快速制备和减阻性能研究 [J/OL]. 表面技术, 1-22[2025-01-20].

[3]李炳炘,张浩,玄克勇,等.微沟槽减阻技术研究现状与进展综述[J]. 煤气与热力, 2023,43(12): 21-27.